IMPLICIT AND EXPLICIT FUNCTION

 FUNCTIONS 

I take it that people who love mathematics are well known with the term function. This blog will go beyond the simple definition of functions. Obviously, we will go through the blurb of functions, but we will focus mainly on two categories of  functions, each distinguished by how the dependent variable is expressed in relation to the independent variable.

A                                  B

visual representation of function

Function

A unique kind of relation from one set (domain) to another set (codomain) is called a function. Let us assume two sets A and B from the above visual representation of function. So a function from A to B is  treated as a relation that assigns a unique element in set B to each element in set A.

Types of functions:

Explicit function:

The functions that define a relationship between an independent variable and a dependent variable which can easily be expressed in terms of other like y = f(x), where y is an independent variable and x is a dependent variable.

No need to worry😟, here are some characteristics by which you can easily identify explicit functions. Here are some of them.

• Isolation of dependent variable: from the simple definition mentioned above, an independent variable can be written in terms of a dependent variable very easily. For example, y = 4x + 5
• Single output from a single input: every input has a unique output, satisfying the function. For instance, if you substitute x = 3, then the value of y = 17.

• Ease of evaluation: since the dependent variables are isolated,      the value of the independent variable can easily be determined.

Here are some examples of explicit functions:

1. y = ln x (log to the base e)

2. y = x^2 + 1

Implicit function:

The function defines a relationship between two or more variables but it is very challenging to represent one variable in terms of another. So it is represented as f(x, y) = 0 instead of y = f(x).

Some characteristics of implicit function:

1. Non-linear relations: generate non-linear relations which makes them difficult to handle algebraically.

2. Multiple values: multiple values of the dependent variable correspond to one independent value.

3. Graphical representation:  the graph of implicit functions may not pass the vertical line test, which is used to determine whether a relation is a function.

Here you go with some interesting examples of implicit functions:

1. Circle :

2. Parabola

3. Hyperbola

Now a question may arise in your mind: why are implicit functions called function when they do not satisfy the definition of functions? The same question arises in my mind as well.

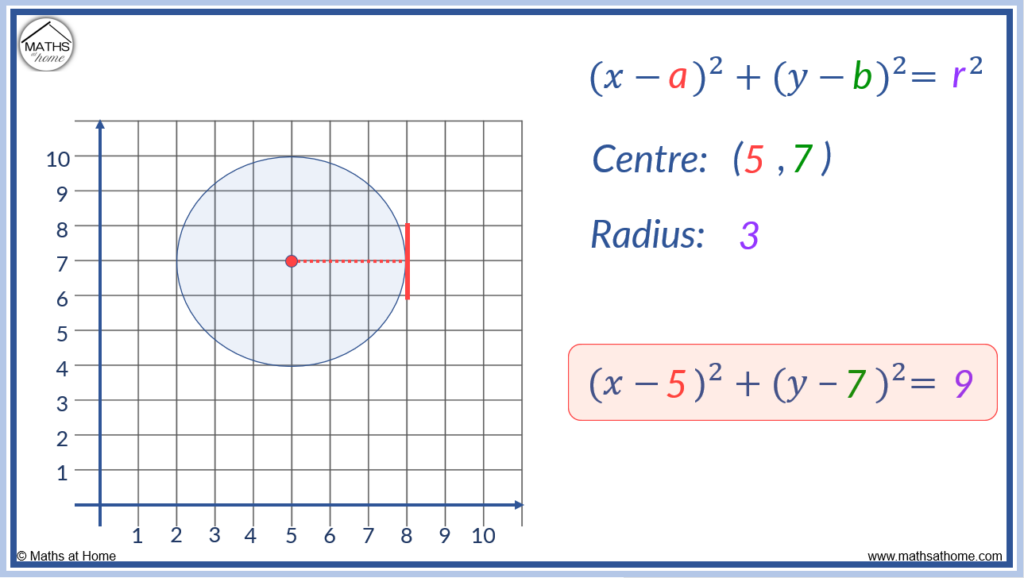
Implicit functions are considered as functions they are used to analyze mathematical relationships between variables and they are not required to be represented explicitly. They give a wider understanding of the relations of variables in mathematics. For instance let us take a example : x^2 + y^2 = 2 (equation of a circle) can be represented as y = sqrt(2 - x^2) or y = - sqrt(2 - x^2) if required in calculation.